Rekursio
Kuten aiemmin on huomattu, funktiot voivat kutsua toisia funktioita. Esimerkiksi näin:
def tervehdi(nimi : str):
print("Moikka,", nimi)
def tervehdi_monesti(nimi : str, kerrat : int):
for i in range(kerrat):
tervehdi(nimi)Samaan tapaan funktio voi kutsua myös itseään. Jos kuitenkaan funktion parametrit eivät muutu kutsukertojen välissä, tästä syntyy "ikuinen silmukka":
def tervehdi(nimi : str):
print("Moikka,", nimi)
tervehdi(nimi)Tällöin funktion kutsuminen millä tahansa merkkijonolla antaa virheilmoituksen:
RecursionError: maximum recursion depth exceeded
Mitä rekursio tarkoittaa?
Virheilmoituksessakin mainitulla rekursiolla tarkoitetaan sitä, että funktio kutsuu itseään. Rekursiossa funktion parametrien pitää kuitenkin muuttua niin, että jossain vaiheessa kutsuminen lopetetaan. Perusperiaate on sama kuin silmukoissa: jotta silmukka ei jatkuisi ikuisesti, siinä tulee olla päättymisehto, joka toteutuu jossain vaiheessa.
Tarkastellaan aluksi yksinkertaista funktiota, joka lisää listan loppuun 0-alkioita niin kauan kuin listan pituus on alle 10. Silmukan sijasta funktio kutsuukin itseään uudestaan, jos ehto ei täyty:
def tayta_lista(luvut: list):
""" Lisää listaan alkoita jos sen pituus on alle 10 """
if len(luvut) < 10:
luvut.append(0)
# Kutsutaan uudestaaan
tayta_lista(luvut)
if __name__ == "__main__":
testi = [1,2,3,4]
tayta_lista(testi)
print(testi)[1, 2, 3, 4, 0, 0, 0, 0, 0, 0]
Perinteisellä silmukalla ohjelma näyttäisi esimerkiksi tältä:
def tayta_lista(luvut: list):
""" Lisää listaan alkoita jos sen pituus on alle 10 """
while len(luvut) < 10:
luvut.append(0)
if __name__ == "__main__":
testi = [1,2,3,4]
tayta_lista(testi)
print(testi)
Esimerkeistä huomataan, että perinteinen (eli iteratiivinen) lähestymistapa tuottaa lyhyemmän ja selkeämmän ohjelman. Rekursiivinen ohjelma kuitenkin toimii ja tuottaa oikean lopputuloksen, koska funktio käsittelee jokaisella kutsukerralla samaa listaa viittauksen kautta.
Rekursio ja paluuarvot
Rekursiivisella funktiolla voi olla myös palautusarvo. Tarkastellaan tätä tarkoitusta varten esimerkkiä, joka laskee kertoman rekursiivisesti:
def kertoma(n: int):
""" Funktio laskee positiivisen luvun n kertoman n!, eli n * (n-1) ... * 2 * 1 """
if n < 2:
# Lukujen 0 ja 1 kertoma on 1
return 1
# Kutsuu funktiota uudestaan
return n * kertoma(n - 1)
if __name__ == "__main__":
# Testataan
for i in range(1, 7):
print(f"Luvun {i} kertoma on {kertoma(i)}")
Luvun 1 kertoma on 1 Luvun 2 kertoma on 2 Luvun 3 kertoma on 6 Luvun 4 kertoma on 24 Luvun 5 kertoma on 120 Luvun 6 kertoma on 720
Jos funktion parametrin arvo on 0 tai 1, funktio palauttaa 1 (koska kertoman määritelmän mukaan lukujen 0 ja 1 kertoma on 1). Muuten funktio palauttaa lausekkeen n * kertoma(n - 1). Tämä tarkoittaa, että parametri n kerrotaan funktion itsensä kutsun palauttamalla arvolla.
Olennaista funktion toimivuuden kannalta on, että funktiossa on määritelty ehto, jolla se ei kutsu itseään enää uudestaan. Tässä tapauksessa ehto on n < 2.
Visualisaattori on oivallinen väline rekursiota käyttävien ohjelmien tutkimiseksi.
Laajennetaan kertoman laskevaa funktiota niin, että se käyttää apumuuttujia:
def kertoma(n: int):
if n < 2:
return 1
edellisen_luvun_kertoma = kertoma(n - 1)
luvun_n_kertoma = n * edellisen_luvun_kertoma
return luvun_n_kertoma
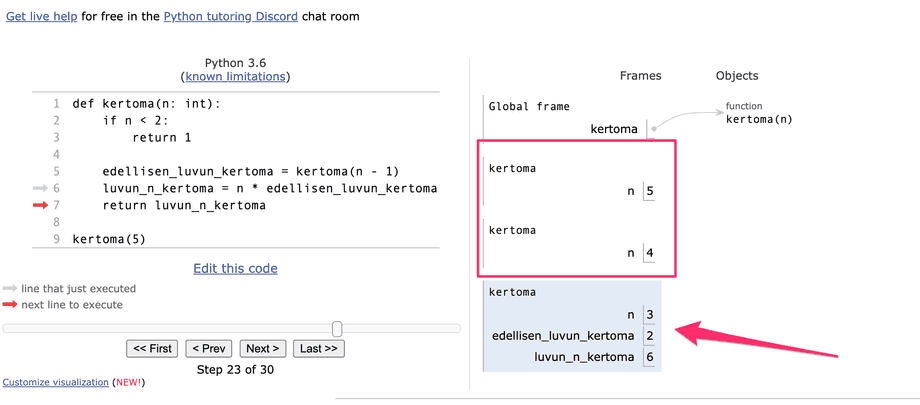
kertoma(5)Kokeile, miten visualisaattori demonstroi rekursion etenemisen.
Hieman normaalista poiketen visualisaattorissa kutsupino "kasvaa" alaspäin. Suorituksessa oleva funktiokutsu on kutsupinon alimpana oleva sinisellä merkitty "lohko", jolla on omat muuttujansa. Hetken kuluttua palautettava tulos on laskettu muuttujaan luvun_n_kertoma.
Tarkastellaan vielä toista funktiota, joka laskee halutun Fibonaccin luvun rekursiivisesti. Fibonaccin lukujonossa luku on aina kahden edellisen luvun summa. Niinpä jonon alku näyttää tältä: 1, 1, 2, 3, 5, 8, 13, 21, 34.
def fibonacci(n: int):
""" Funktio palauttaa n:nen luvun Fibonaccin sarjasta (1, 1, 2, 3, 5, 8 jne.); n > 0"""
if n <= 2:
# Kaksi ekaa lukua ovat ykkösiä
return 1
# Muuten luku saadaan laskemalla kaksi edellistä yhteen
return fibonacci(n - 1) + fibonacci(n - 2)
# Testataan, että toimii
if __name__ == "__main__":
for i in range(1, 11):
print(f"Fibonaccin {i}. luku on {fibonacci(i)}")Fibonaccin 1. luku on 1 Fibonaccin 2. luku on 1 Fibonaccin 3. luku on 2 Fibonaccin 4. luku on 3 Fibonaccin 5. luku on 5 Fibonaccin 6. luku on 8 Fibonaccin 7. luku on 13 Fibonaccin 8. luku on 21 Fibonaccin 9. luku on 34 Fibonaccin 10. luku on 55
Tällä kertaa lopetusehtona on, että luku on pienempi tai yhtä suuri kuin 2, koska Fibonaccin kaksi ensimmäistä lukua ovat molemmat ykkösiä.
Miten algoritmi käytännössä oikein toimii?
Luvuille 1 ja 2 algoritmi palauttaa arvon 1 ehdon n <= 2 mukaisesti.
Luvulle 3 algoritmi palauttaa arvon lausekkeesta fibonacci(n - 1) + fibonacci(n - 2), eli käytännössä lausekkeen fibonacci(2) + fibonacci(1). Koska edellisessä kohdassa huomattiin, että näiden molempien arvo on 1, palauttaa funktio siis arvon 2 (joka onkin kolmas Fibonaccin luku)
Luvulle 4 algoritmi palauttaa arvon lausekkeesta fibonacci(3) + fibonacci(2), mikä edellisten kohtien perusteella on siis 2 + 1 eli 3.
Luvulle 5 algoritmi palauttaa arvon lausekkeesta fibonacci(4) + fibonacci(3), mikä edellisten kohtien perusteella on siis 3 + 2 eli 5.
jne.
Rekursiivinen algoritmimme siis toimii, koska voimme todistaa jokaisen luvun kohdalla ohjelman toimivuuden aikaisempien lukujen perusteella.
Binäärihaku
Binäärihaussa yritetään löytää järjestyksessä olevasta listasta annettu alkio. Järjestys tarkoittaa tässä yhteydessä esimerkiksi lukujen järjestystä pienimmästä suurimpaan tai merkkijonoja aakkosjärjestyksessä.
Binäärihaun ideana on, että tarkastellaan aina listan keskimmäistä alkiota. Jos
- keskimmäinen alkio on etsitty alkio, palautetaan tieto siitä, että alkio löytyi
- keskimmäinen alkio on pienempi kuin etsittävä alkio, rajataan haku listan jälkimmäiselle puolikkaalle
- keskimmäinen alkio on suurempi kuin etsittävä alkio, rajataan haku listan ensimmäiselle puolikkaalle
Jos lista on tyhjä, palautetaan tieto siitä, että alkiota ei löytynyt.
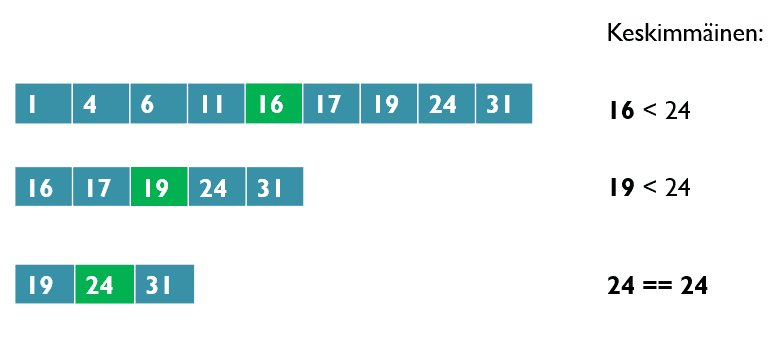
Seuraava kuva havainnollistaa binäärihaun etenemistä, kun etsitään listasta lukua 24:
Rekursiivinen algoritmi binäärihaulle:
def binaarihaku(lista: list, alkio: int, vasen : int, oikea : int):
""" Funktio palauttaa True tai False sen mukaan, onko listalla alkiota """
# Jos hakualue on tyhjä, ei löydy
if vasen > oikea:
return False
# Lasketaan hakualueen keskikohta
keski = (vasen+oikea)//2
# Jos keskellä on etsittävä alkio
if lista[keski] == alkio:
return True
# Jos pienempi, etsi jälkipuoliskolta
if lista[keski] < alkio:
return binaarihaku(lista, alkio, keski+1, oikea)
# Muuten täytyy olla suurempi, etsitään alkupuoliskolta
else:
return binaarihaku(lista, alkio, vasen, keski-1)
if __name__ == "__main__":
# Testataan
lista = [1, 2, 4, 5, 7, 8, 11, 13, 14, 18]
print(binaarihaku(lista, 2, 0, len(lista)-1))
print(binaarihaku(lista, 13, 0, len(lista)-1))
print(binaarihaku(lista, 6, 0, len(lista)-1))
print(binaarihaku(lista, 15, 0, len(lista)-1))True True False False
Tässä funktiolle binaarihaku annetaan neljä parametria: viite listaan, etsittävä alkio sekä hakualueen vasen ja oikea kohta. Alussa hakualue on koko lista, jolloin vasen kohta on 0 ja oikea kohta on len(lista)-1. Funktio tarkastaa hakualueen keskellä olevan alkion ja joko ilmoittaa, että haluttu alkio löytyi, tai jatkaa hakua vasemmasta tai oikeasta puoliskosta.
Jos verrataan binäärihakua peräkkäishakuun, algoritmien tehokkuus erottuu selvästi. Peräkkäishaussa alkiota lähdetään etsimään listan alusta ja listaa käydään läpi yksi alkio kerrallaan, kunnes alkio on löytynyt tai on päästy listan loppuun. Jos listan pituus on miljoona alkiota, tarvitaan perättäishaussa koko listan läpikäyntiin miljoona askelta, mutta binäärihaussa askelia tarvitaan vain 20.